全文共2948字，预计学习时长9分钟

图源：superprof

伟大的前苏联物理学家列夫·朗道和叶夫根尼·利夫希茨在他们的著作《经典场论》中写道：“建立在相对论基础上的引力场理论被称为广义相对论，它是由爱因斯坦建立的，并且可能是现存的物理理论中最美丽的一个。”

所有认真研究过广义相对论的人都会觉得它具有一种独特的吸引力。20世纪最具影响力的物理学家之一、英国理论物理学家保罗·狄拉克曾说过：

“很难将牛顿引力理论与其力的瞬时传播相协调，使之符合狭义相对论的要求；然而，爱因斯坦却解决了这一问题，相对论理论也由此诞生——这可能是有史以来最伟大的科学发现。”

本文中，笔者将结合昌德拉塞卡的文章（任何遗漏或不清楚的细节都可以在作品文章中找到），并试图说明为何这些伟大科学家都做出了如此有力的陈述。

图源：unsplash

仔细观察下图：

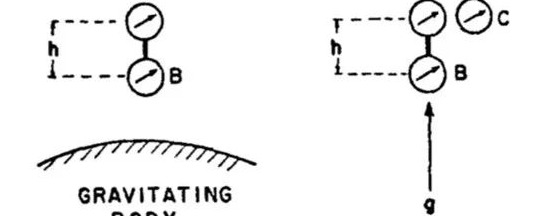
根据等效原理，时钟A和时钟B将根据时钟C保持相同的相对时间。

当时钟向上移动时，根据狭义相对论，时钟A和时钟B测量的时间间隔与真空中的时钟C测量的相应间隔具有以下关系：

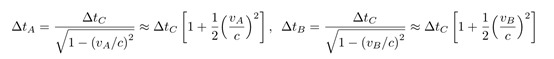
结合这两个表达式，可以得到：

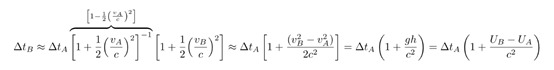
在以上方程中还使用到了托里拆利公式和引力势的概念：

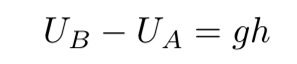
现在，如果把时钟B放到没有引力场的位置x上，那么上面的表达式将变成：

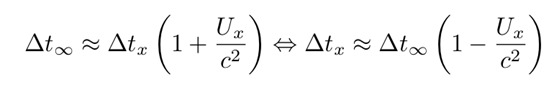
公式1：两次的时间间隔如何随引力势U（x）的变化而变化。

在牛顿力学中，有两种概念的质量，即惯性质量和引力质量。前者是一种测量外力阻力的方法（根据牛顿第二定律）。后者是引力场的来源，也是另一个大质量物体对引力场的反应。

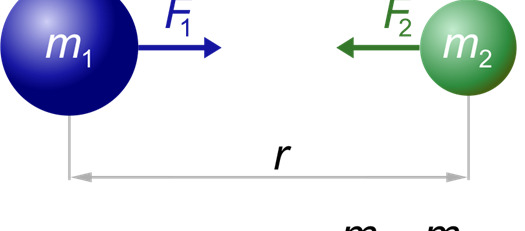
根据牛顿万有引力定律，此图展示了相互吸引的两个物体。

两个质量分别为M与m的物体相距R，它们之间的引力可表示为：

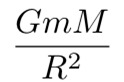
根据牛顿第二定律，物体m（或M）的加速度为：

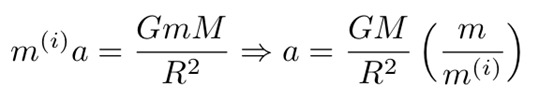
公式2：惯性质量和引力质量之所以会相等，是因为加速度的大小并不取决于物体的质量。因为加速度是不变的，所以质量比必须是常数。很明显，此时该常数为1。

事实上，加速度a的大小无关于质量m，这也意味着上述的质量比是一个普适常数。由此推断，惯性质量和引力质量的大小相等。

在狭义相对论中，闵可夫斯基距离表现为以下形式：

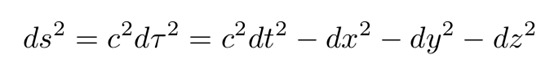
公式3：狭义相对论中的闵可夫斯基距离。

其中dτ表示其本征时间。沿世界线的本征时间（物体在时空中的轨迹）是由沿着该线的时钟测量出的时间。

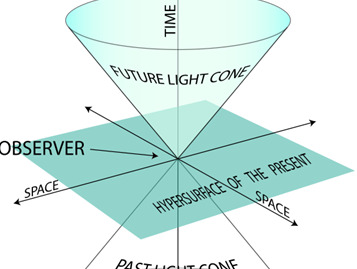
对于给定的事件，该图显示了闵可夫斯基时空的四个不相交细分。

如上图所示，时空中的世界线可以有以下三种：

· 光速曲线，每一点都表示光速。这样的世界线在时空中形成了一个光锥。

· 时间曲线。这些速度小于光速的曲线落在光锥内（注意：大质量粒子的世界线都是时间型曲线）

· 空间曲线。例如，这些曲线表示物体的长度。

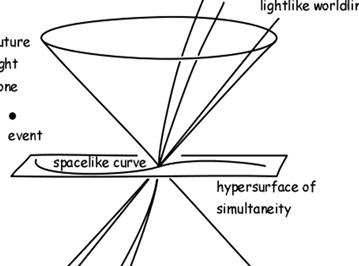
以上各种世界线皆对应一种dτ的符号。

本征时间dτ的长短取决于时空的性质。在时空的某个区域，如果方程2有效，那么就可以将其代入方程3，并得出：

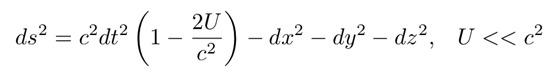
公式4：由恒定引力场引起的闵可夫斯基时空间隔的变化。

现在，可以考虑进行坐标变换，将其放入一个匀加速的参考系中。新的x和t变成：

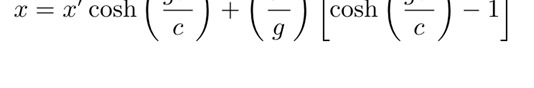
公式5：通过坐标变换将其放入一个匀加速的参考系。

y和z保持不变。闵可夫斯基区间方程3用该坐标表示如下：

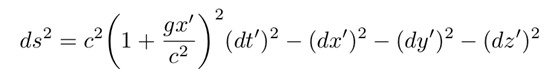
公式6：匀加速的参考系中的闵可夫斯基距离。

现在，在变换方程5中选择时间小于或等于c/g的次数，并进行简单展开，即新的时空间隔方程3变成：

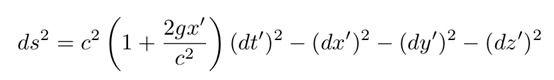
公式7：用非惯性坐标表示的平直闵可夫斯基时空中的时空间隔。

注意，它的形式与方程4相同。因此，根据等效原理，转换成一个加速参考系相当于引入一个引力场。

图源：unsplash

到目前为止，我们只考虑了闵可夫斯基度量下的小偏差。与爱因斯坦相同，我们也假设，一般来说（不仅是小偏差）引力场的存在扭曲了时空的几何结构。更准确地说，爱因斯坦的引力理论认为，在引力场存在的情况下，时空会成为一个光滑的伪黎曼流形，并具有以下形式的时空间隔：

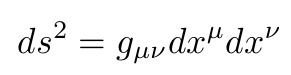
公式8：伪黎曼流形上的时空间隔。

在闵可夫斯基时空中，粒子以匀速直线运动：

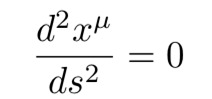
公式10：在闵可夫斯基时空中，粒子以匀速直线运动。

在没有重力的情况下，让我们把下列变换成一个曲线坐标系：

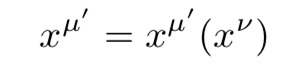
公式11：在没有重力的情况下转换成曲线坐标。

时空间隔变为：

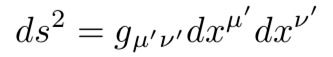
方程12：变换后的时空间隔方程11。

其中：

方程13：变换后的度量张量公式11。

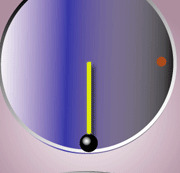
在上图的惯性参考系中，黑球以直线运动。然而，站在旋转参照系（底部）中的观察者（红点）看到，由于该参照系中存在科里奥利力和离心力，该黑球沿着弯曲的路径行进。

运动方程10成为普遍存在的测地线方程：

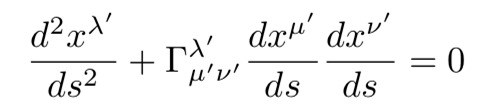
方程14：运动方程10经坐标变换后变为方程11，此时仍然没有重力。

其中物体被称为克氏符号。

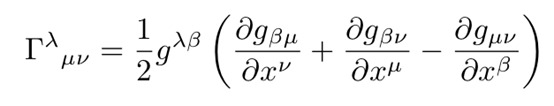
方程15：在测地线方程中出现的克氏符号。

在方程14中，克氏符号产生一种“明显的”加速度，这种加速度只是在用曲线坐标描述笛卡尔坐标系中的线性运动时产生的。但它们实际上是惯性加速度（例如科里奥利加速度）。

但是根据等价原理，所有的加速度，无论是惯性加速度还是重力加速度，都是度量：重力扭曲了时空几何（这是一个具有相关度量的拟黎曼流形），并且粒子在时空中沿着方程16给出的测地线进行运动。

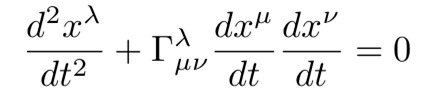
方程16：粒子在时空中运动所依据的测地线运动方程。

在牛顿物理学中，描述引力场的方程是用引力势U来表示的。当没有引力时，只有U=0；当有一个大质量物体，但受其场影响的被测粒子在物体外时，有∇²U=0；在有物质的区域，方程变为∇²U=4πGρ。

再试试如何把这三个方程应用于广义相对论。

首先，假设有一个粒子根据方程16来进行运动。如果方程16通过坐标转换可变为方程10，那么这就意味着粒子不在引力场中。

同样，在目前的重力下，克氏符号在任何坐标变换后都不能消失。利用克氏符号的变换规律就很容易证明，如果要通过一个普通的坐标变换来使得所有的克氏符号都消失，只有当方程17中的四个变换fs对于方程18有解。

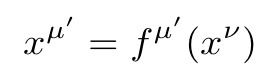
方程17：应用于克氏符号的变换。

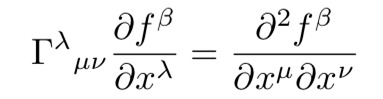
方程18：克氏符号消失的条件。

如果所谓的黎曼-克氏张量消失，就会发生这种情况。后者由以下给出：

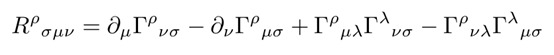
方程19：黎曼曲率张量或黎曼-克氏张量。

我们得出结论，引力场不存在的条件是：

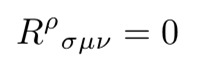
方程20：失重的条件。这个方程是U=0牛顿方程在相对论理论下的结果。

这个方程是牛顿方程U=0的广义相对论版本。可见，∇²U=0最简单的概括是方程20的收缩，即：

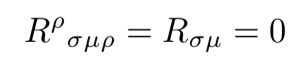
方程21：里奇标量的消失是∇²U=0牛顿方程在相对论下的结果。

这个消失的物体叫做里奇张量。最后一步是确定∇²U=4πGρ右侧的归纳。在此，首先想到的是能量动量张量。通过狭义相对论，我们可以知道它的导数消失了。但是广义相对论是协变理论，所以标准导数的消失是不够的：我们还需要T的协变导数消失，并且这在所有坐标系中都满足。

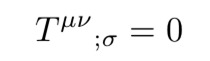
但里奇张量的协变导数是非零的。通过引入一个相关且协变导数会消失的张量，即所谓的爱因斯坦张量，这一问题就会得以解决。

在广义相对论中，物体之间的引力效应是时空扭曲的结果。

因此，爱因斯坦引力定律变成：

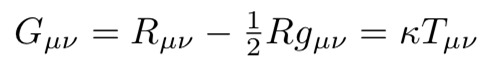
通过要求在c → ∞的区间内，可以获得常数k，并且牛顿的理论也能得以应用。

最美丽的物理理论，你感受到它的魅力了嘛？

留言点赞关注

我们一起分享AI学习与发展的干货

如转载，请后台留言，遵守转载规范

制图网(www.makepic.net)，专业的logo免费设计在线生成网站，全自动智能化logo设计，商标设计，logo在线生成！

欢迎使用制图网制作属于您公司自己的logo，不仅专业而且经济实惠，全方位满足您公司品牌化、视觉化的需求。